Наши партнеры

Энциклопедический словарь Брокгауза и Ефрона.
Дробь, в математике

Дробь, в математике

Дробь. — Если делится какое-нибудь целое число а на другое целое число b, т. е. ищется число x, удовлетворяющее условию bx = а, то могут представиться два случая: или в ряду целых чисел найдется число х, которое этому условию удовлетворит, или же окажется, что такого числа х не существует. Поэтому, если ограничиться рассмотрением совокупности одних целых чисел, то задача деления одного целого числа на другое будет разрешаться только в некоторых частных случаях; вообще же решение ее будет невозможно. Это обстоятельство заставляет ввести в круг нашего рассмотрения новую область чисел — дробей.

Условимся принимать, что каждым двум целым числам а и b соответствует одна дробь, которую и обозначим  целое число а назовем числителем Д.  а число b — знаменателем ее. Условимся две Д.  и  считать равными только тогда, если можно найти два таких целых числа m и n, чтобы удовлетворились условия: am = cn и bm = dn. Отсюда следует, что  

На этом основывается первая операция с дробями — сокращение: если числитель и знаменатель Д.  имеют общего множителя l, то Д. может быть представлена в виде: Д. называется несократимою, если числитель и знаменатель ее не имеют общего множителя. Вместе с тем на основании введенных условий всегда возможно две Д. —  и  — привести к общему знаменателю и к общему числителю. Условимся считать Д.  больше  , если по приведении к общему знаменателю N = mb = nd, числитель первой Д. ma будет больше числителя второй nc; и наоборот, пусть  если ma < nc; равным образом, если Д.  и  приведены к общему числителю М = m′a = n′c, то Д.  будет больше или меньше Д.  смотря по тому, будет число m′b меньше или больше числа n′d. Из этого определения следует, что Д.  будет увеличиваться, если ее числитель будет увеличиваться или ее знаменатель будет уменьшаться, и наоборот.

Суммой двух или нескольких Д., имеющих общего знаменателя, назыв. Д., знаменатель которой равен сему общему знаменателю, а числитель — сумме числителей. Чтобы составить сумму нескольких Д., имеющих различные знаменатели, надлежит привести их к общему знаменателю. Из этого определения вытекает, что сумма Д. не зависит от порядка сложения Д., что сумма более каждого слагаемого и т. д. Вычитание Д. определяется как действие, коим по заданной сумме двух Д. и одному из слагаемых требуется определить другое слагаемое.

Произведением двух дробей  и наз. дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей. Из этого определения следует, между прочим, что произведение не зависит от порядка множителей, что произведение увеличивается или уменьшается с увеличением или уменьшением одного из множителей и т. д. Разумея под частным двух Д.  и  Д. x, удовлетворяющую условию  сейчас же убеждаемся, что деление дроби на Д. всегда возможно, т. е. действительно дает Д. 

Так как всякое целое число N может быть рассматриваемо как Д.  , то деление целого числа на целое в области дробей всегда возможно; намеченная обобщением понятия целого числа цель оказывается достигнутой. Иногда рассматривают Д. как меру частей целого. Такое рассмотрение основывается на следствиях, вытекающих из приведенных выше определений суммы и произведения дробей: Д.  взятая слагаемым m раз, дает единицу; равным образом произведение  на m дает также единицу; поэтому Д. — может быть принята за меру одной m^-ой части единицы, а Д.  — за меру n m^-ых частей ее. В этом смысле умножение какого-нибудь числа А на Д. есть взятие n m^-ых частей этого числа, а деление А на  есть отыскание числа, n m^-ых частей которого равны А.

Д. назыв. правильною, если числитель ее меньше знаменателя; Д. называется неправильною, если, наоборот, числитель больше знаменателя; так,  есть правильная, а  неправильная Д.; если неправильная Д. представлена в виде суммы целого числа и правильной Д., то такая Д. наз. смешанной Д., или смешанным числом: напр.  есть смешанное число.

Десятичною наз. Д., знаменатель которой есть десять или степень десяти; напр.  есть десятичная Д. Десятичные Д. обыкновенно представляют иначе, пользуясь тем принципом, на котором основано изображение многозначных целых чисел (т. е. что цифра, стоящая вправо, в десять раз меньше цифры, стоящей влево от первой) и распространяя это условие на части единицы. На этом основании, напр., Д.  изображается 0,377 — где запятая означает, что стоящие вправо от нее цифры соответствуют частям единицы. Такое обозначение значительно упрощает все действия над десятичными дробями. Обыкновенная Д. может быть обращена в десятичную тогда и только тогда, если по приведении ее к несократимому виду знаменатель ее будет заключать множителями только 2 и 5, т. е. будет вида  Наоборот, если знаменатель дроби  по приведении к несократимому виду будет содержать другие, кроме 2 и 5, множители, то обыкновенная Д. не может быть обращена в десятичную. С другой стороны, всегда возможно найти такую десятичную Д., чтобы разность между заданной обыкновенной Д.  и десятичной была менее всякой произвольно взятой величины ε. Пусть, напр.,   чтобы найти десятичную Д., удовлетворяющую условию и  надо разделить  на b; пусть , где остаток ε < b; в таком случае очевидно  и

Если нужно найти такую десятичную Д., чтобы разность между  и этой дробью была меньше где n > m, то достаточно разделить  на b, т. е. продолжить указанное вычисление еще на несколько знаков; таким образом новая Д. будет заключать в первых m разрядах те же цифры, что и ранее найденная; увеличение степени приближения не изменяет уже найденных при меньшем приближении цифр соответствующей десятичной Д. Если показатель m в  (степени приближения десятичной дроби к заданной обыкновенной) достаточно велик, то десятичная Д. будет заключать в своем выражении периодическое повторение цифр; напр., если m = 12, то соответствующая десятичная Д. 1,142857142857.

Разность между обыкновенной Д.  и соответствующей ей десятичной, в которой увеличиваем число периодов, уменьшается и при достаточном повторении периода может быть сделана менее всякой наперед заданной величины. В этом смысле говорят, что всякая обыкновенная Д., которая не может быть обращена в конечную десятичную Д., обращается в бесконечную периодическую Д. и в этом смысле пишут напр.  или 

Периодические Д. бывают простые (чистые) и смешанные. Простыми периодическими Д. наз. те, у коих период начинается с первой после запятой цифры; смешанными же наз. те Д., перед началом периода коих встречаются другие цифры, в период не входящие. Простая периодическая Д. получается от обращения обыкновенной Д., у которой в знаменатель не входят совсем множители 2 и 5. Обратно, если знаменатель обыкновенной., по приведении ее к несократимому виду заключает множителей 2 или 5, то соответствующая периодическая Д. будет смешанною.

Нахождение по заданной периодической дроби той обыкновенной дроби, которой она соответствует, производится по следующим правилам: для обращения чистой (простой) периодической дроби надо период разделить на число, в котором цифра 9 повторяется столько раз, сколько цифр в периоде. Чтобы найти соответствующую смешанной периодической Д. обыкновенную, нужно числитель последней положить равным разности чисел, взятых до 2-го и 1-го периода данной Д., а в знаменателе повторить цифру 9 столько раз, сколько цифр в периоде, и приписать справа. столько нулей, сколько цифр до периода.

Алгебрическою Д. называется выражение вида  , где под а и b разумеются какие угодно величины.

Д. показатели — см. Показатель.

Д. дифференцирование — см. Интегральное исчисление.

Непрерывные Д. Непрерывными Д. называются выражения вида

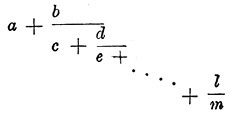
Если числа а, b, с,.... l, m — целые и положительные, то непрер. Д. называется арифметическою; если же это какие угодно величины — то алгебраическою.

Создателем исчисления непрерывных Д. является знаменитый голландский математик Гюйгенс (Huyghens); до него около половины XVII века одним любителем математики, лордом Брункером, была дана без доказательства и без указаний на свойства непрерывных Д. следующая формула для приближенного вычисления отношения одной восьмой части окружности к ее радиусу:

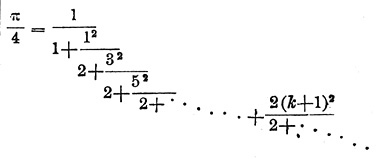
Гюйгенс же, в мемуаре «Descriptio automati planetarii», напечатанном в 1680 г., не только указал на главнейшие свойства непрерывных Д., но и дал весьма остроумное приложение этих свойств к определению числа зубцов на колесах модели планетной системы. Дальнейшее развитие теории непрерывных Д. дано Эйлером и особенно Лагранжем; последнему принадлежит честь введения в анализ алгебраических непр. Д. При помощи свойств этих Д. оказалось возможным решение многих весьма сложных вопросов, к коим неприложимы методы исчисления бесконечно малых (дифференциального и интегрального исчислений); поэтому применение теории алгебраических непрерывных Д. к различным вопросам анализа послужило предметом замечательных по остроумию методов и по достигнутым результатам мемуаров ряда ученых с Гауссом и Чебышевым во главе. Для истории русской математической литературы эта теория имеет тем больший интерес, что наиболе существенные результаты (после Лагранжа и Гаусса) достигнуты в ней известным русским математиком П. Л. Чебышевым и его учениками.

Разложение обыкновенных Д. в непрерывные. Пусть дана обыкновенная несократимая Д. a/b; если поступать с числами а и b как поступают при отыскании общего наибольшего их делителя последовательным делением (см. Деление), то получится такой ряд равенств:

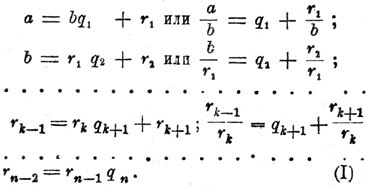
Здесь все числа q и r положительны; при этом b> r₁,> r₂ >... > r_n-1; поэтому мы дойдем непременно до остатка r_n, равного нулю. На основании уравнений (I) для a/b получается конечная непрерывная Д.:

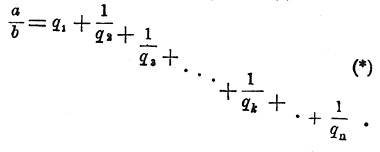
Числа q₁, q₂, q₃,... q_k,... q_n называются первым, вторым, третьем, k^-ым, n^-ым неполными частными непрерывной Д. a/b; числа b/r₁, r₁/r₂,... r_n—2/r_n—1, которые в дальнейшем будут обозначаться через p₁, p₂,... p_n—1 называются первым, вторым, третьим,... n—1^-ым полными частными непр. Д.

Обыкновенные Д.

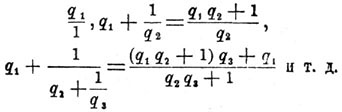
называются первою, второю, третьей и т. д. подходящими дробями к a/b. Не трудно видеть, что Д. a/b больше первой, третьей, вообще нечетной подходящей Д., и меньше второй, четвертой, вообще четных подходящих дробей.

Д. a/b всегда заключается между двумя подходящими дробями.

Обозначим числителя и знаменателя k^-той подходящей к a/b Д. через Р_k и Q_k. В таком случае:

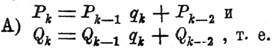
числитель k^-той подходящей Д. равен произведению числителя k — 1 подходящей Д. на k^-тое неполное частное, сложенному с числителем k — 2^-ой подходящей Д.; а знаменатель k^-ой подходящей Д. равен произведению знаменателя k—1^-ой Д. на k^-тое неполное частное, сложенному с знаменателем k—2^-ой подходящей Д.

и Б)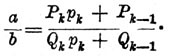

Для доказательства положений достаточно проверить их справедливость для первых подходящих дробей и затем убедиться, что если правило справедливо для некоторого значка а, то оно будет справедливо и при k+1. Из этих формул вытекают такие следствия:

1) Все числа Р_k и Q_k положительны и притом

P_n>P_n—1>... >P_k>... P₂>P₁

Q_n>Q_n—1>... >Q_k>... >Q₁

2) Разность двух подходящих дробей по численной величине равна единице, деленной на произведение знаменателей этих дробей, т. е.

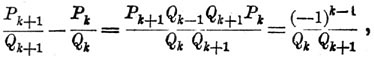
3) Разность P_n/Q_n — a/b

по численной величине менее

1/(Q_n Q_n+1) или 1/Q_n²

4) Каждая последующая подходящая Д. более приближается к величине a/b, чем предшествующая.

и 5) Подходящая Д. более приближается к значению Д. a/b, чем всякая другая Д., знаменатель которой меньше знаменателя подходящей дроби.

Простейшее приложение непрерывных дробей — решение в целых числах неопределенного уравнения:

ах — by = с, (**)

где а, b, с — числа целые, положительные, причем а и е взаимно простые. Пусть a/b разлагается в непрерывную Д. (*), так что

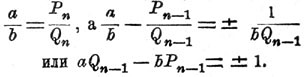
Если n — число нечетное, то надо взять при единице знак —, и в таком случае очевидно

х = с (b — Q_n—1), y = c (a — P_n—1)

будут решениями ур-ния (*); если n четное, то надо взять при единице знак +, и тогда

x = cQ_n—1, у = сР_n—1

будут решениями ур-ния (**). Все прочие решения найдутся из формул х+bk, y+ak, давая k значения целые между —∞ и +∞; решения ур-ния ах + by = c найдутся по тому же приему, по замене у на —у₁

Разложения иррациональных чисел в непрерывные Д.: пусть А — число иррациональное и пусть q₁ есть целое число, ближайшее к А и меньше A; положим A = q₁+ ¹/a₁; число а₁> о и также иррациональное (иначе А было бы рациональное); пусть q₂ есть целое число, ближайшее к а₁ и меньшее а₁; положим а₁ = q₂ + ¹/a₂; поступая таким же образом с а₂, a₃... и т. д., мы получим ряд равенств

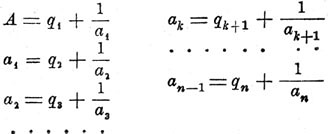
откуда находим для А такую непрер. Д.

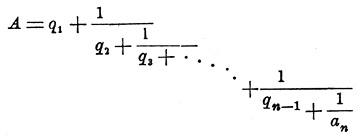
Если через P_k/Q_k обозначить k^-тую подходящую Д. этой непрерывной Д., то при k четном A < P_k/Q_k, при к нечетном А > P_k/Q_k и т. д.; вообще все указанные выше теоремы будут совершенно применимы и здесь. Можно еще доказать, что при достаточно большом n разность между А и P_n/Q_n по численной величине может быть сделана менее всякой наперед заданной величины ε. В самом деле, по численной величине

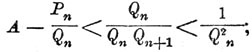
поэтому, если

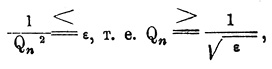
то эта разность действительно меньше ε; но числа Q₁ = q₁, Q₂,... Q_n — числа целые и возрастающие; поэтому при достаточно большом n Q_n может быть сделано больше всякой наперед заданной величины, следовательно и больше 1/√ε; теорема таким образом будет доказана; на основании этой теоремы говорят, что всякое иррациональное число А может быть обращено в бесконечную непрерывную Д, и обозначают засим

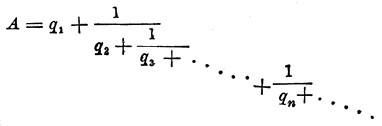
Если число А удовлетворяет квадратному уравнению с рациональными (целыми или дробными) коэффициентами, т. е. если аА² + bA + с = 0 (a, b и с — числа рациональные), то соответствующая бесконечная непрерывная Д. будет периодическою, и наоборот.

С. Савич.